Find the intervals in which the function f given by

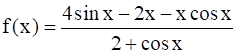
is (i) strictly increasing (ii) strictly decreasing.

(i) It is given that f(x) =

Now, if f’(x) =0

⇒ cos x = 0 or cosx = 4

But, cosx = 4 is not possible

Therefore, cosx =0

⇒ x =

Now, x = divides (0,2π) into three disjoints intervals

In the intervals and, f’(x)>0

Therefore, f(x) is increasing for 0< x < and < x < 2π.

In interval, f’(x)<0

Therefore, f(x) is decreasing for < x < .