Prove that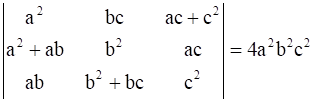

Given,

LHS =

RHS = 4a²b²c²

LHS = Δ =

Taking out common factors a, b and c from C₁, C₂ and C₃, we have

Δ = abc

Applying Elementary Transformations

R₂→ R₂ – R₁ and R₃→ R₃ – R₁

Δ = abc

R₂→ R₂ + R₁

Δ = abc

R₃→ R₃ + R₂

Δ = abc

Δ = 2ab²c

C₂→ C₂ – C₁

Δ = 2ab²c

Expanding along R₃ we get,

Δ = 2ab²c [a (c – a) + a (a + c)]

= 2ab²c [ac – a² + a² + ac]

= 2ab²c (2ac)

= 4a²b²c²

Δ = RHS

∴ LHS = RHS

Hence, Proved