If 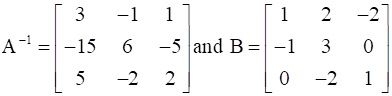, find (AB)^-1

B =

We need to find B^-1

To find the inverse of a matrix we need to find the Adjoint of that matrix

For finding the adjoint of the matrix we need to find its cofactors

Let B_ij denote the cofactors of Matrix B

Minor of an element b_ij = M_{ij �}

b₁₁ = 1, Minor of element b₁₁ = M₁₁ = = (3 × 1) – ((-2) × 0) = 3

b₁₂ = 2, Minor of element b₁₂ = M₁₂ = = ((-1) × 1) – (0 × 0) = -1

b₁₃ = -2, Minor of element b₁₃ = M₁₃ = = ((-1) × (-2)) – (3 × 0) = 2

b₂₁ = -1, Minor of element b₂₁ = M₂₁ = = (2 × 1) – ((-2) × (-2)) = -2

b₂₂ = 3, Minor of element b₂₂ = M₂₂ = = (1 × 1) – ((-2) × 0) = 1

b₂₃ = 0, Minor of element b₂₃ = M₂₃ = = (1 × (-2)) – (2 × 0) = -2

b₃₁ = 0, Minor of element b₃₁ = M₃₁ = = (2 × 0) – ((-2) × 3) = 6

b₃₂ = -2, Minor of element b₃₂ = M₃₂ = = (1 × 0) – ((-2) × (-1)) = -2

b₃₃ = 1, Minor of element b₃₃ = M₃₃ = = (1 × 3) – (2 × (-1)) = 5

Cofactor of an element b_ij, B_ij = (-1)^i+j × M_ij

B₁₁ = (-1)¹⁺¹× M₁₁ = 1 × 3 = 3

B₁₂ = (-1)¹⁺²× M₁₂ = (-1) × (-1) = 1

B₁₃ = (-1)¹⁺³× M₁₃ = 1 × 2 = 2

B₂₁ = (-1)²⁺¹× M₂₁ = (-1) × (-2) = 2

B₂₂ = (-1)²⁺² × M₂₂ = 1 × 1 = 1

B₂₃ = (-1)²⁺³ × M₂₃ = (-1) × (-2) = 2

B₃₁ = (-1)³⁺¹ × M₃₁ = 1 × 6 = 6

B₃₂ = (-1)³⁺² × M₃₂ = (-1) × (-2) = 2

B₃₃ = (-1)³⁺³ × M₃₃ = 1 × 5 = 5

Adj B = =

|B| = 1 (3 × 1 – (-2) × 0) – 2 ((-1) × 1 – 0 × 0) + (-2) ((-1) × (-2) – 3 × 0)

|B| = 3 – 2 ( -1 – 0) – 2 (2 – 0)

|B| = 3 + 2 – 4 = 1

∴ B^-1 = (Adj B)/|B| = /1 =

We know (AB)^-1 = B^-1A^-1

(AB)^-1 = ×

Solving the above matrix we get

(AB)^-1 =