Prove that 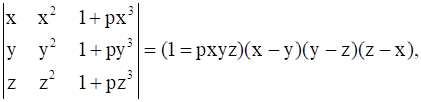where p is any scalar.

Let Δ =

Applying Elementary Row Transformations

R₂→ R₂ – R₁ and R₃→ R₃ – R₁

Δ =

Taking (y – x) and (z – x) common from R₂ and R₃ respectively

Δ = (y – x) (z – x)

Applying R₃→ R₃ – R₂

Δ = (y – x) (z – x)

Taking (z – y) common from R₃

Δ = (y – x) (z – x) (z – y)

Expanding along R₃, we have

Δ = (x – y) (y – z) (z – x) [0 – 1 {x × p(y² + x² + xy) – 1 × (1 + px³)} + p (x + y + z) {x × (y + x) – 1 × x²}

Δ = (x – y) (y – z) (z – x) (-px³ – pxy² – px²y + 1 + px³ + px²y + pxy² + pxyz)

Δ = (x – y) (y – z) (z – x) (1 + pxyz)

Hence, the given result is proved.