Prove that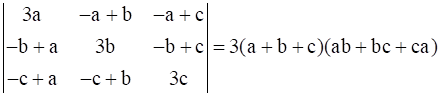

Let Δ =

Applying Elementary Transformations

C₁→ C₁ + C₂ + C₃, we have

Δ =

Taking (a + b + c) common from C₁, we get

Δ = (a + b + c)

Applying R₂→ R₂ – R₁ and R₃→ R₃ – R₁

Expanding along C₁

Δ = (a + b + c) [1 × {(2b + a) (2c + a) – (a – b) (a – c)} – 0 + 0]

Δ = (a + b + c) [4bc + 2ab + 2ac + a² – a² + ac + ba – bc]

Δ = (a + b + c) (3ab + 3bc + 3ac)

Δ = 3 (a + b + c) (ab + bc + ca)

Hence, the given result proved.