Find the matrix X so that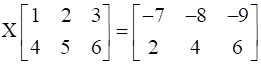

Given X

From above equation it can be observed that matrix on R.H.S is a 2×3 matrix and that on the L.H.S is also a 2×3 matrix. Therefore, X must be a 2×2 matrix.

Let X

So the equation is given by:

Now equating the corresponding elements of both the matrices we get,

a + 4b = -7, 2a + 5b = -8, 3a + 6b = -9

c + 4d = 2, 2c + 5d = 4, 3c + 6d = 6

Now, a + 4b = -7 ⇒ a = -4b -7

∴ 2a + 5b = -8 ⇒ 2.(-4b -7) + 5b = -8

⇒ -8b -14 + 5b = -8

⇒ -3b = 6

⇒ b = -2

∴ a = -4b -7 ⇒ a = -4.(-2) -7

⇒ a = 1

Now, c + 4d = 2 ⇒ c = -4d + 2

∴ 2c + 5d = 4 ⇒ 2.(-4d + 2) + 5d = 4

⇒ -8d + 4 + 5d = 4

⇒ -3d = 0

⇒ d = 0

∴ c = -4d + 2 ⇒ c = -4.0 + 2

⇒ c = 2

Thus, a = 1, b = -2, c = 2, d = 0.

Hence X becomes