Calculate the depression in the freezing point of water when 10 g of CH₃CH₂CHClCOOH is added to 250 g of water. K_a = 1.4 × 10^–3, K_f = 1.86 K kg mol^–1.

Question

Calculate the depression in the freezing point of water when 10 g of CH 3 CH 2 CHClCOOH is added to 250 g of water. K a = 1.4 × 10 –3 , K f = 1.86 K kg mol –1 .

Philoid · Accepted Answer

Given: Mass of CH₃CH₂CHClCOOH = 10 g

Mass of water = 250g

K_a = 1.4 × 10^–3,

K_f = 1.86 K kg mol^–1

Molar mass of CH₃CH₂CHClCOOH = 12 + 3 + 12 + 2 + 12 + 1 + 35.5 + 2 + 16 + 16 + 1

= 122.5 g mol^–1

Number of moles of solute =

→ No. of moles =

∴ No. of moles = mol

Now, Molality is given as,

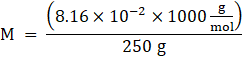
M = 0.3264 kg/mol

CH₃CH₂CHClCOOH CH₃CH₂CHClCOO^- + H ⁺

Initial moles	1	0	0
Equilibrium moles	(1-α)	α	α

Total moles at equilibrium = (1-α) + 2 α

= 1 + α

In order to find out the depression in freezing point, _f_f values of i(vant Hoff’s factor) and α(degree of dissociation) are to be found out.

To find out degree of dissociation, _α

→

Here, the value of α is negligible as compared to 1, and hence 1- = 1, giving,

→

∴

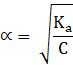
To find out Vant Hoff’s factor,

→

∴

Now, to find out the depression in freezing point,

_f_f

∴

Thus, the depression in freezing point is _f = 0.65⁰C

Calculate the depression in the freezing point of water when 10 g of CH3CH2CHClCOOH is added to 250 g of water. Ka = 1.4 × 10–3, Kf = 1.86 K kg mol–1.

Calculate the depression in the freezing point of water when 10 g of CH₃CH₂CHClCOOH is added to 250 g of water. K_a = 1.4 × 10^–3, K_f = 1.86 K kg mol^–1.