Find the roots of each of the following equations, if they exist, by applying the quadratic formula:

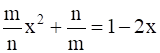
Given:

taking LCM m²x+ n² = mn – 2mnx

On cross multiplying

m²x+ 2mnx + n² – mn = 0

Comparing with standard quadratic equation ax² + bx + c = 0

a = m², b = 2mn, c = n² – mn

Discriminant D = b² – 4ac

= (2mn)² – 4.m². (n² – mn)

= 4m²n² – 4m²n² + 4m³n > 0

Hence the roots of equation are real.

Roots α and β are given by

Hence the roots of equation are