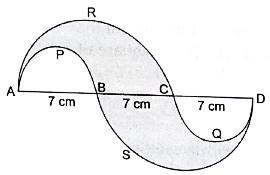
In the given figure, APB and CQD are semicircle of diameter 7 cm each, while ARC and BSD are semicircles of diameter 14 cm each. Find the (i) perimeter, (ii) area of the shaded region.

(i) Given:

Diameter of semicircles APB and CQD = 7 cm

⇒ Radius of semicircles APB and CQD = cm = r₁

Diameter of semicircles ARC and BSD = 14 cm

⇒ Radius of semicircles ARC and BSD = cm = 7 cm = r₂

Perimeter of APB = Perimeter of CQD

Area of APB = Area of CQD ………….. (i)

Perimeter of ARC = Perimeter of BSD

Area of ARC = Area of BSD ………….. (ii)

∵ Perimeter of semicircle = πr …………… (iii)

∴ Perimeter of APB = πr₁

= × = 11 cm

Then, using (i), we have

Perimeter of CQD = 11 cm

Now, using (iii), we have

Perimeter of ARC = πr₂

= × 7 = 22 cm

Then, using (ii), we have

Perimeter of BSD = 22 cm

Perimeter of shaded region

= (Perimeter of ARC + Perimeter of APB) + (Perimeter of BSD + Perimeter of CQD)

= (22 + 11) + (22 + 11) = 33 + 33 = 66 cm

Hence, the perimeter of the shaded region is 66 cm.

(ii) Now,

∵ Area of semicircle = πr² …………. (iv)

∴ Area of APB = πr₁²

= × × × = cm²

Then, using (i), we have

Area of CQD = cm²

Now, using (iv), we have

Area of ARC = πr₂²

= × × 7 × 7 = 11 × 7 = 77 cm²

Then, by using (ii), we have

Area of BSD = 77 cm²

Area of shaded region

= (Area of ARC-Area of APB) + (Area of BSD- Area of CQD)

= (77 - ) + (77 - )

= () + () = + = = 115.5 cm²

Hence, the area of the shaded region is 115.5 cm².