In the given figure, OPQR is a rhombus, three of whose vertices lie on a circle with centre O. If the area of the rhombus is 32√3 cm2, find the radius of the circle.
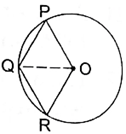
Here in the given figure ‘O’ is the centre of circle on which three vertices of rhombus lie, this implies that OP, OR are both radius of the circle. Also we know that in rhombus all the 4 sides are equal in length. Thus OP, OR, PQ, RQ, they all are radii of circle. Also OQ is equal to radius of circle. Now rhombus being a parallelogram therefore diagonal OQ will divide the rhombus into two equal halves this means that the area of triangle OQR will be equal to half of the area of rhombus. Also we can see that triangle OQR is an equilateral triangle and hence we can easily calculate its area in terms of radius of circle and equate it to half of the area of rhombus and calculate the radius of given circle.
![]()
Let the radius of the circle = x cm
Now join OQ

Consider ∆OQR,
OQ = OR = RQ = x cm
⇒ ∆OQR is an equilateral triangle
![]()
Where a = side of equilateral triangle
Also we know OQ is a diagonal of rhombus OPQR and as in a parallelogram diagonal divides it into two equal area or halves , similarly OQ is also dividing the rhombus into two equal areas therefore,
⇒ Area of ∆OQR = Area of ∆OPQ → eqn2
Area of OPQR = Area of ∆OQR + Area of ∆OPQ
Area of OPQR = 2 × Area of ∆OQR (from eqn2) → eqn3
Put the values of area of OPQR and equation 1 in equation 3
![]()
![]()
![]()
![]()
![]()
![]()
![]()
As every quadratic equation has two roots, similarly x2 = 64 also have two roots i.e. x = 8 and x = -8. As we know that ‘x’ represents radius of circle therefore it cannot be a negative value, hence we discard the negative root.
Therefore radius of the circle = x = 8 cm.
The radius of circle is 8 cm.