The difference between the sides at right angles in a right-angled triangle is 7 cm. The area of the triangle is 60 cm². Finds its perimeter.

Let the sides at right angles be a and b

And, the third side be c.

Given: a-b = 7 cm

Area of triangle = 60 cm²

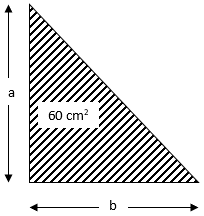
Now, since a-b = 7

⇒ a = b + 7

Now we know that,

Area of triangle = 1/2 × base × height

⇒ 60 = 1/2 × b × (b + 7)

⇒ 60 × 2 = b² + 7b

⇒ b² + 7b = 120

⇒ b² + 7b – 120 = 0

⇒ b² + 15b - 8b – 120 = 0

⇒ b(b + 15) - 8(b + 15) = 0

⇒ (b + 15)(b-8) = 0

This gives us two equations,

i. b – 8 = 0

⇒ b = 8

ii. b + 15 = 0

⇒ b = -15

Since, the side of the triangle cannot be negative

Therefore, b = 8 cm

⇒ a = (b + 7) cm

⇒ a = (8 + 7) cm

⇒ a = 15 cm

Now we know that,

Base² + Perpendicular² = Hypotenuse²

⇒ a² + b² = c²

⇒ 15² + 8² = c²

⇒ c² = 225 + 64

⇒ c² = 289

⇒ c = 17

Now,

Perimeter of triangle = a + b + c

⇒ Perimeter of triangle = 15 + 8 + 17

⇒ Perimeter of triangle = 40 cm