The tops of two towers of heights x and y, standing on a level ground subtend angles of 30° and 60° respectively at the centre of the line joining their feet. Then, x : y is

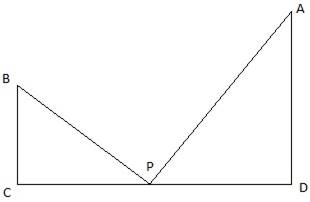
Let BC = x and AD = y be the two towers. They subtend angles 30° and 60° at the centre of the line joining their feet say P. Join C, P, D. Also join B, P and A, P. So, ∠BPC = 30° and ∠APD = 60°. Also, we get two right-angled triangles BPC and APD with right angles at C and D respectively. We have to find x:y.

From ∆BPC,

or,

or,

From ∆APD,

or,

or,

y = PD√3

So, taking the ratio we get,

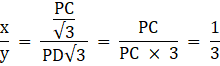
Hence, the correct choice is C.