Show that the line segment which joins the midpoints of the oblique sides of a trapezium is parallel to the parallel sides.

Question

Philoid · Accepted Answer

We can draw the trapezium as

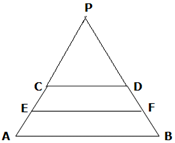
Here, let EF be the line segment joining the oblique sides of the trapezium at midpoints E and F (say) correspondingly.

Construction: Extend AD and BC such that it meets at P.

To Prove: EF ∥ DC and EF ∥ AB

Proof: Given that, ABCD is trapezium which means DC ∥ AB. …(statement (i))

In ∆PAB,

DC ∥ AB (by statement (i))

So, this means we can apply Thale’s theorem in ∆PAB. We get

…(ii)

∵ E and F are midpoints of AD and BC respectively, we can write

DA = DE + EA

Or DA = 2DE …(iii)

CB = CF + FB

Or CB = 2CF …(iv)

Substituting equation (iii) and (iv) in equation (ii), we get

⇒

By applying converse of Thale’s theorem, we can write DC ∥ EF.

Now if DC ∥ EF, and we already know that DC ∥ AB.

⇒ EF is also parallel to AB, that is, EF ∥ AB.

This means, DC ∥ EF ∥ AB.

Hence, proved.