In the given figure, side BC of ΔABC is bisected at D and O is any point on the AD. BO and CO produced meet AC and AB at E and F respectively, and the AD is produced to X so that D is the midpoint of OX. Prove that AO: AX = AF: AB and show that EF || BC.

We have the diagram as,
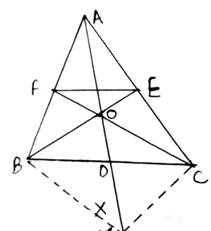
Given: BD = DC & OD = DX
To Prove: ![]() and also, EF ∥ BC
and also, EF ∥ BC
Proof: Since, from the diagram we can see that diagonals OX and BC bisect each other in quadrilateral BOCX. Thus, BOCX is a parallelogram.
If BOCX is a parallelogram, BX ∥ OC, and BO ∥ CX.
⇒ BX ∥ FC (as OC extends to FC) and CX ∥ BE (BO extends to BE)
⇒ BX ∥ OF and CX ∥ OE
∵ BX ∥ OF, applying Thale’s theorem in ∆ABX, we get
![]() …(i)
…(i)
Now since CX ∥ OE, applying Thale’s theorem in ∆ACX, we get
![]() …(ii)
…(ii)
By equations (i) and (ii), we get
![]()
By applying converse of Thale’s theorem in the above equation, we can write
EF ∥ BC
Hence, proved.