Find the length of altitude AD of an isosceles ΔABC in which AB = AC = 2a units and BC = a units.
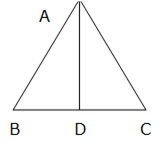
Δ ABC is an isosceles triangle.
Also, AB = AC = 2a
The AD is the altitude. Therefore, D is the midpoint of BC.
![]()
ΔADB and ΔADC are right-angled triangles.
Applying Pythagoras theorem,
AB2 = BD2 + AD2
![]()
![]()
![]()
10