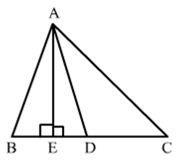
In ΔABC, D is the midpoint of BC and AE ⊥ BC. If AC > AB, show that
AB² = AD² — BC • DE + 1/4 BC²

Question

In ΔABC, D is the midpoint of BC and AE ⊥ BC. If AC > AB, show that AB 2 = AD 2 — BC • DE + 1/4 BC 2

Philoid · Accepted Answer

In right-angled triangle AED, applying Pythagoras theorem,

AB² = AE² + BE²

⇒ AE² = AB² – BE² ….(i)

In right-angled triangle AED, applying Pythagoras theorem,

AD² = AE² + ED²

⇒ AE² = AD² – ED² ….(ii)

Therefore,

AB² – BE² = AD² – ED²

In ΔABC, D is the midpoint of BC and AE ⊥ BC. If AC > AB, show thatAB2 = AD2 — BC • DE + 1/4 BC2