In ΔABC, AB = AC. Side BC is produced to D. Prove that (AD² - AC²) = BD • CD.

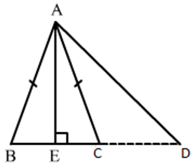
Draw AE⊥BC. Applying Pythagoras theorem in right-angled triangle AED,

Since, ABC is an isosceles triangle and AE is the altitude and we know that the altitude is also the median of the isosceles triangle.

So, BE = CE

And DE + CE = DE + BE = BD

AD² = AE² + ED²

⇒AE² = AD² - ED² …(i)

In ΔACE,

AC² = AE² + EC²

⇒ AE² = AC² –EC² …(ii)

Using (i) and (ii),

⇒ AD² - ED² = AC² –EC²

⇒ AD² - AC² = ED²–EC²

⇒ AD² - AC² = (DE + CE) (DE – CE)

⇒ AD² - AC² = (DE + BE) CD

⇒ AD² - AC² = BD.CD