In an equilateral triangle with side a, prove that area = .

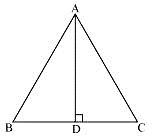
Let ABC be the equilateral triangle whose side is a cm.

Let us draw altitude AD(h) such that AD ⊥ BC.

We know that altitude bisects the opposite side.

So, BD = DC = a cm.

In ADC, ∠ADC = 90°.

We know that the Pythagoras Theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

So, by applying Pythagoras Theorem,

AC² = AD² + DC²

(a cm)² = AD² + (a/2 cm)²

a² cm² = AD² + a²/4 cm²

AD² = 3a²/4 cm²

AD = √3 a/2 cm = h

We know that area of a triangle = 1/2 × base × height

Ar(ΔABC) = 1/2 × a cm × √3 a/2 cm

⇒ ar(ΔABC) = √3 a²/4 cm²

Hence proved.

ar(ΔABC) = √3 a²/4 cm²