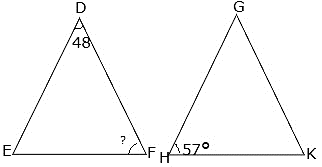
Two triangles DEF and GHK are such that ∠D = 48° and ∠H = 57°. If ΔDEF ≅ ΔGHK then find the measure of ∠F.

Question

Two triangles DEF and GHK are such that ∠ D = 48° and ∠ H = 57°. If ΔDEF ≅ ΔGHK then find the measure of ∠ F.

Philoid · Accepted Answer

Given that ΔDEF ≅ ΔGHK.

We know that if in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion) and hence the two triangles are similar (AAA criteria).

∴ ∠D = 48° = ∠G

∠H = 57° = ∠E

∠F = ∠K = x°

We know that the sum of angles in a triangle = 180°.

So, in ΔDEF,

⇒ 48° + 57° + x° = 180°

⇒ 105° + x° = 180°

⇒ x° = 180° - 105°

⇒ x° = 75° = ∠F

Ans. ∠F = 75^o