If the lengths of the sides BC, CA and AB of a ΔABC are a, b and c respectively and AD is the bisector of ∠A then find the lengths of BD and DC.

Question

If the lengths of the sides BC, CA and AB of a ΔABC are a, b and c respectively and AD is the bisector of ∠ A then find the lengths of BD and DC.

Philoid · Accepted Answer

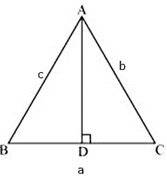
Given that ΔABC is the triangle whose sides are AB = c, AC = b, BC = a

And AD is the bisector of ∠A.

We know that altitude bisects the opposite side.

So, let BD = DC = x.

Since AD bisects ∠A,

AC/AB = CD/DB

Substituting the given values,

b/c = CD/(a-CD)

Cross multiplying,

⇒ b( a – CD) = c (CD)

⇒ ba – b(CD) = c (CD)

⇒ ba = CD (b + c)

⇒ CD = ba/ (b + c)

Since CD = BD,

BD = ba/ (b + c)

BD = ba/(b + c) and DC = ba/(b + c)