Two poles of height 13 m and 7 m respectively stand vertically on a plane ground at a distance of 8 m from each other. The distance between their tops is
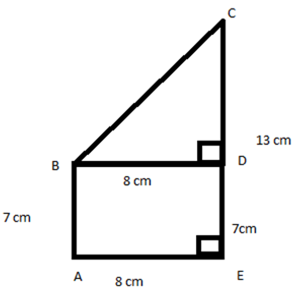
Let AB and CE be the two poles of the height 13 cm and 7 cm each which are perpendicular to the ground. The distance between them is 8 cm.
Now since CE and AB are ⊥ ground AE
BD ⊥ to CE and BD = 8 cm
Top of pole AB is B and top of pole CE is C
Now Δ BDC is right angled at D and BC, the hypotenuse is the distance between the top of the poles and CD = 13 – 7 = 6
(BC)2 = (BD) 2 + (CD)2
⇒ (BC)2 = 64 + 36
⇒ (BC)2 = 100
⇒ (BC)= 10 cm
The distance between the top of the poles is 10 cm
2