In a triangle, the perpendicular from the vertex to the base bisects the base. The triangle is

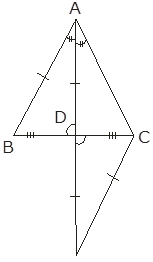
In Δ ABC, AD bisects ∠ A and meets BC in D such that BD = DC

Extend AD to E and join C to E such that CE is ∥ to AB

∠ BAD = ∠ CAD

Now AB ∥ CE and AE is transversal

∠ BAD = ∠ CED (alternate interior ∠s)

But ∠ BAD = ∠ CED = ∠CAD

In Δ AEC

∠ CEA = ∠CAE

∴ AC = CE………………. 1

In Δ ABD and Δ DCE

∠BAD = ∠CED (alternate interior ∠s)

∠ADB = ∠ CDE (vertically opposite ∠s)

BD = BC (given)

Δ ABD ≅ Δ DCE

AB = EC (CPCT)

AC = EC (from 1)

⇒AB = AC

⇒ ABC is an isosceles Δ with AB = AC