In the given figure, ΔABC and ΔDBC have the same base BC. If AD and BC intersect at O, prove that 

Given: ∆ ABC and ∆ DBC have the same base BC.
AD and BC intersect at O.
To show: ![]()
First, we construct the altitudes, AE and DF, of ∆ ABC and ∆ DBC, respectively.
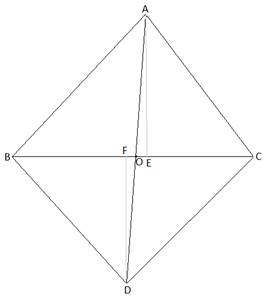
Consider, ∆ AOE and ∆ DOF,
∠DFO = ∠AEO [Right angles]
∠DOF = ∠AOE [Vertically Opposite angles]
So, by AA criterion,
∆AOE ∼ ∆DOF
⇒ Ratio of all the corresponding sides of ∆ AOE and ∆ DOF are equal.
![]() ……….(i)
……….(i)
Now, we know that
![]()
![]() ……….(ii)
……….(ii)
Similarly, ![]() ……….(iii)
……….(iii)
Dividing (ii) by (iii),
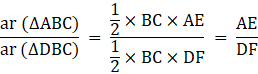
![]()
![]() [From (i)]
[From (i)]
17