In the given figure, XY || AC and XY divides ΔABC into two regions, equal in area. Show 

Given: XY ∥ AC
ar (∆ XBY) = ar (XACY) ……….(i)
To show: ![]()
Consider ∆ ABC, XY ∥ AC
So, Using Basic Proportionality theorem, we have
![]() ……….(ii)
……….(ii)
Now, in ∆ XBY and ∆ ABC,
∠XBY = ∠ABC [common angle]
![]() [Using (ii)]
[Using (ii)]
⇒ ∆ XBY ∼ ∆ ABC [By SAS criterion]
Now, we know that the ratios of the areas of two similar triangles are equal to the ratio of squares of any two corresponding sides.
![]()
From (i), we have
ar (∆ XBY) = ar (XACY)
Let ar (∆ XBY) = x = ar (XACY) ⇒ ar (∆ ABC) = ar (∆ XBY) + ar (XACY) = x + x = 2x
![]()
![]()
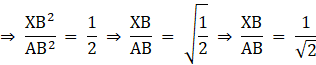
Now, we know that
XB = AB – AX
![]()
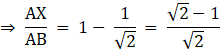
Rationalizing the denominator, we have
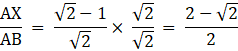
![]()
18