Using integration find the area of region bounded by the triangle whose vertices are (– 1, 0), (1, 3) and (3, 2).

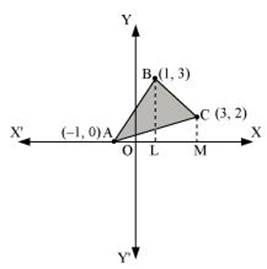
BL and CM are drawn perpendicular to x – axis.

We can see that from the figure that,

Area(ΔACB) = Area(ALBA) + Area(BLMCA) - Area(AMCA) …(1)

Now, equation of line segment AB is

Thus, Area(ALBA) =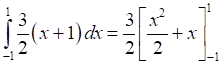

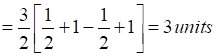
Now, equation of line segment BC is

Thus, Area (BLMCB) =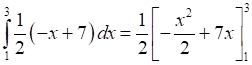

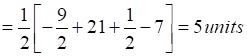
Now, equation of line segment AC is

Thus, Area (AMCA) =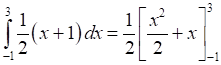

Now putting all these values in equation (1), we get,

Area(ΔABC) = (3 + 5 – 4) = 4 units.