In fig. 4, a triangle ABC is drawn to circumscribe a circle of radius 2 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 4 cm and 3 cm respectively. If the area of Δ ABC=21cm², then find the lengths of sides AB and AC.

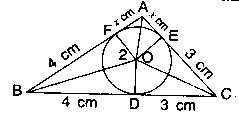
First, we join OB, OF, OA, OE, and OC.

D, E, and F are the tangent points.

As we know that Tangents to a circle
from a point are equal.

So, BF= BD = 4 cm (given)

CE= CD= 3 cm (given)

AF=AE= x cm (assume)

We are also given that area of Δ ABC=21cm²

Now,

area(Δ ABC) = area(Δ BOC) + area(Δ COA) + area(Δ AOB)

area (Δ BOC) = 1/2 × Base(BC) × Height(OD)
= 1/2 × 7 × 2=7cm²

area(Δ COA) = 1/2 × Base(AC) × Height(OE)
= 1/2 × (3 + x) × 2= 3 + x

area(Δ AOB) = 1/2 × Base(AB) × Height(OF)
= 1/2 × (4 + x) × 2= 4 + x

Putting the values in the equation;
area(Δ ABC) = area(Δ BOC) + area(Δ COA) + area(Δ AOB)

⇒ 21=7 + 3 + x + 4 + x

⇒ 21=14 + 2x

⇒ 7=2x

⇒ x=3.5cm

∴ Length of AB= 4 + x = 4 + 3.5= 7.5cm

And, Length of AC = 3 + x= 3 + 3.5=6.5cm