In fig. 6, arcs are drawn by taking vertices A, B and C of an equilateral triangle ABC of side 14 cm as centers to intersect the sides BC, CA and AB at their respective mid-points D, E and F. Find the area of the shaded region.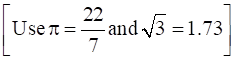

Given that D, E and F are midpoints of BC, AC and AB respectively.

AF = 1/2 AB= 1/2 (14)=7cm

As ABC is an equilateral triangle, ∠A = ∠B = ∠C = 60°

Area of shaded region = Area(ΔABC)-Area(AFE)-Area(BFD)-Area(CDE)

As these are arcs we have to find area of sector=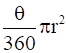

As ∠A = ∠B = ∠C = 60°, θ =60° for all three sectors

Also, radius =AF=7cm for all three sectors

∴ Area of shaded region= Area(Δ ABC)-3Area(AFE)

=

=

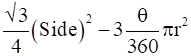
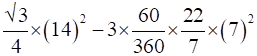
=84.77 – 77 =7.77cm²