For each of the differential equations in question, find the particular solution satisfying the given condition:

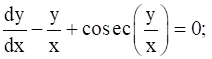y = 0 when x = 1

Here, putting x= kx and y = ky

= k⁰.f(x,y)

Therefore, the given differential equation is homogeneous.

To solve it we make the substitution.

y = vx

Differentiating eq. with respect to x, we get

Integrating both sides, we get

- cosv = - logx + C

y = 0 when x = 1

- 1 = C

The required solution of the differential equation.