For each of the differential equations given in question, find the general solution:

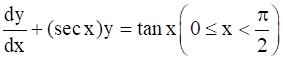
It is given that

This is equation in the form of (where, p = secx and Q = tanx)

Now, I.F. =

Thus, the solution of the given differential equation is given by the relation:

y(I.F.) =

⇒ y(secx + tanx) = secx + tanx – x+ C

Therefore, the required general solution of the given differential equation is

y(secx + tanx) = secx + tanx – x+ C.