Probability that A speaks truth is 4/5. A coin is tossed. A reports that a head appears. The probability that actually there was head is
Given: let E1 be the event that A speaks truth, E2 be the event that A lies and X be the event that it appears head.
Therefore, ![]()
As E1 and E2 are the events which are complimentary to each other.
Then P (E1) + P (E2) = 1
⇒ P (E2) = 1 - P (E1)
⇒ P (E2) ![]()
If a coin is tossed it may show head or tail.
Hence the probability of getting head is 1/2 whether A speaks a truth or A lies.
P(X|E1) = P(X|E2) = 1/2
Now the probability that actually there was head, give that A speaks a truth is P(E1|X).
By using bayes’ theorem, we have:
![]()
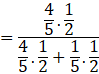
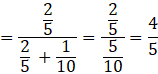
![]()
Therefore correct answer is (A).
14