The random variable X has a probability distribution P(X) of the following form, where k is some number:

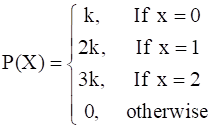
(a) Determine the value of k.

(b) Find P (X < 2), P (X ≤ 2), P(X ≥ 2).

Given: A random variable X with its probability distribution.

(a) As we know the sum of all the probabilities in a probability distribution of a random variable must be one.

Hence the sum of probabilities of given table:

⇒ k + 2k + 3k + 0 = 1

⇒ 6k = 1

(b) (i) P(X < 2) = ?

P(X < 2) = P(X = 0) + P(X = 1)

= k + 2k

= 3k

(ii) P(X ≤ 2) = ?

P(X ≤ 2) = P(X = 0) + P(X = 1) + P(X = 2)

= k + 2k + 3k

= 6k

(iii) P(X ≥ 2) = ?

P(X ≥ 2) = P(X = 2) + P(X > 2)

= 3k + 0

= 3k