Two numbers are selected at random (without replacement) from the first six positive integers. Let X denote the larger of the two numbers obtained. Find E(X).

Question

Philoid · Accepted Answer

Given: first six positive integers.

Two numbers can be selected at random (without replacement) from the first six positive integer in 6 × 5 = 30 ways.

X denote the larger of the two numbers obtained. Hence, X can take any value of 2, 3, 4, 5 or 6.

For X = 2, the possible observations are (1, 2) and (2, 1)

For X = 3, the possible observations are (1, 3), (3,1), (2,3) and (3, 2).

For X = 4, the possible observations are (1, 4), (4, 1), (2,4), (4,2), (3,4) and (4,3).

For X = 5, the possible observations are (1, 5), (5, 1), (2,5), (5,2), (3,5), (5,3) (5, 4) and (4,5).

For X = 6, the possible observations are (1, 6), (6, 1), (2,6), (6,2), (3,6), (6,3) (6, 4), (4,6), (5,6) and (6,5).

Hence, the required probability distribution is,

X	2	3	4	5	6
P(X)

Therefore E(X) is:
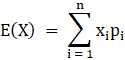