In a meeting, 70% of the members favour and 30% oppose a certain proposal. A member is selected at random and we take X = 0 if he opposed, and X = 1 if he is in favour. Find E(X) and Var (X).
Given: X = 0 if members oppose, and X = 1 if members are in favour.
P(X = 0) ![]()
P(X = 1) ![]()
Hence, the required probability distribution is,
X | 0 | 1 |
P(X) | 0.3 | 0.7 |
Therefore E(X) is:
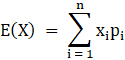
= 0 × 0.3 + 1 × 0.7
⇒ E(X) = 0.7
And E(X2) is:

= (0)2 × 0.3 + (1)2 × 0.7
⇒ E(X2) = 0.7
Then Variance, Var(X) = E(X2) – (E(X))2
= 0.7 – (0.7)2
= 0.7 – 0.49 = 0.21
15