In Fig. 4, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.

Or

In Fig. 5, the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB.

Question

Philoid · Accepted Answer

We have figure,

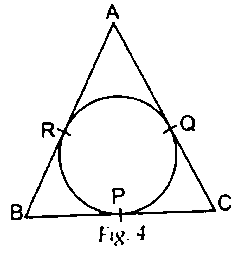
Given: AB = AC and ∆ABC circumscribe a circle with the circle touching the side AB at R, AC at Q and BC at P.

To Prove: P bisects the side of the triangle, BC.

⇒ BP = PC

Proof: ∵, RB and BP are tangents to the circle from the same point. ⇒ BP = BR …(i)

QC and CP are tangents to the circle from the same point. ⇒ QC = CP …(ii)

Also, RA and AQ are tangents to the circle from the same point. ⇒ AQ = AR …(iii)

Adding equations (i), (ii) and (iii), we get

BP + QC + AQ = BR + CP + AR

⇒ (AQ + QC) + BP = (AR + BR) + CP

⇒ AC + BP = AB + CP

⇒ BP = CP [∵, BP = CP]

Or

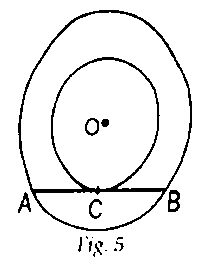
Given: A chord AB of the larger of the two concentric circles having mid-point O, touching the smaller circle at point C.

To prove: AC = AB

Construction: Join O to C.

Proof: AB is tangent to the inner circle and OC is meeting AB at C.

⇒ ∠OCB = ∠OCA = 90°, which means that OC is perpendicular to AB.

AB is also the chord of the outer circle, on which OC is perpendicular to.

∵, According to the chord theorem, the perpendicular from the centre of a circle to a chord bisects the chord.

Thus, this only justifies that OC bisects AB at the point of its contact.

⇒ AC = CB

Hence, proved.

In Fig. 4, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.OrIn Fig. 5, the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB.