Prove that the parallelogram circumscribing a circle is a rhombus.

Question

Philoid · Accepted Answer

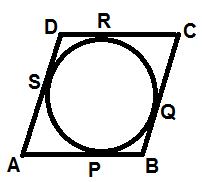
We know that-

Opposite Sides of a ||gm should be equal.

∴ AB = CD and AD = BC …(1)

In the above fig,

AP and AS are making a pair of tangents drawn from vertex A of ||gm ABCD on the circle.

∴ AP = AS…(2)

[∵ Tangents drawn from an exterior point to the circle are equal in length]

BP and BQ are making a pair of tangents drawn from vertex B of ||gm ABCD on the circle.

∴ BP = BQ…(3)

[∵ Tangents drawn from an exterior point to the circle are equal in length]

CR and CQ are making a pair of tangents drawn from vertex C of ||gm ABCD on the circle.

∴ CR = CQ…(4)

[∵ Tangents drawn from an exterior point to the circle are equal in length]

DS and DR are making a pair of tangents drawn from vertex C of ||gm ABCD on the circle.

∴ DR = DS…(5)

[∵ Tangents drawn from an exterior point to the circle are equal in length]

Adding equations (2),(3),(4) and (5), we get-

AP+BP+CR+DR = AS+BQ+CQ+DS

⇒ (AP+BP)+(CR+DR) = (AS+DS)+(BQ+CQ)

⇒ AB+CD = AD+BC

⇒ 2AB = 2BC [From (1)]

∴ AB = BC …(6)

From (1) and (6), we get-

AB=BC=CD=DA

∴ ||gm ABCD is a rhombus.

Hence, the parallelogram circumscribing a circle is a rhombus.