D is a point on the side BC of ΔABC such that ∠ADC and ∠BAC are equal. Prove that: CA² = DC x CB.

Question

D is a point on the side BC of ΔABC such that ∠ ADC and ∠ BAC are equal. Prove that: CA 2 = DC x CB.

Philoid · Accepted Answer

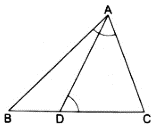
Given:

ADC = BAC

D is a point on the side BC

∠ACB = ∠ACD (Common Angle)

So ΔABC & ΔADC are similar by the A.A. (Angle-Angle) axiom of Similarity

Since the two triangles are similar so their lengths of sides must be in proportion

Cross Multiplying We Get

CA² = DC x CB

Which is the required expression

Hence Proved

D is a point on the side BC of ΔABC such that ∠ADC and ∠BAC are equal. Prove that: CA2 = DC x CB.