Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of an equilateral triangle described on one of its diagonals.

Question

Philoid · Accepted Answer

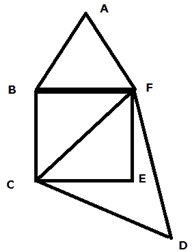
Let us assume BFEC is a square , ΔABF is an equilateral triangle described on the side of the square & Δ CFD is an equilateral triangle describes on diagonal of the square

Now since ΔABF & Δ CFD are equilateral so they are similar

Let side CE = a,

So EF = a

CF² = a² + a²

CF² = 2a²

Since both the triangles are similar so according to the Area –Length relations of similar triangle we can write

⇒

So Area Of Δ CFD = 2 ΔABF

Hence Proved