Prove that the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
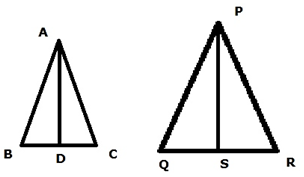
Let us assume ΔABC & ΔPQR are similar
Area of ΔABC = 0.5 ×AD ×BC
Area of ΔPQR = 0.5 ×PS ×QR
Now since the two triangles are similar so the length of sides and perpendiculars will also be in proportion
![]() …Equation 1
…Equation 1
![]() …Equation 2
…Equation 2
From Equation 1 We get
![]()
Putting in Equation 2 we get
![]()
⇒ ![]()
So we can see ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides
Hence Proved
26