If f is a function satisfying f (x + y) = f(x) f(y) for all such that

f(1) = 3 and 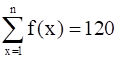, find the value of n.

It is given that,

f (x + y) = f (x) × f (y) for all x, y ∈ N … (1)

f (1) = 3

Taking x = y = 1 in (1), we obtain

f (1 + 1) = f (2) = f (1) f (1) = 3 × 3 = 9

Taking x = 1 and y = 2 in (1), we obtain

f (1 + 2) = f (3) = f (1) f (2) = 3 × 9 = 27

Similarly, Taking x = 1 and y = 3 in (1), we obtain

f (1 + 3) = f (4) = f (1) f (3) = 3 × 27 = 81

∴ f (1), f (2), f (3), …, that is 3, 9, 27, …, forms a G.P. with both the first term and common ratio equal to 3.

We know that -

Sum of first n terms of G.P with first term 'a' and common ratio 'r' is given by -

It is known that,

But,

∴ n = 4

Thus, the value of n is 4.