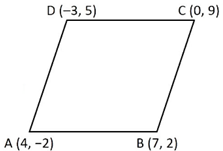
The points A(4, –2), B(7, 2), C(0, 9) and D(–3, 5) form a parallelogram. Find the length of the altitude of the parallelogram on the base AB.

We have

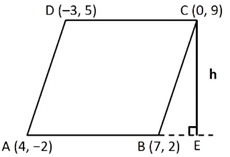
We need to find length of the altitude of the parallelogram on the base AB. Re-drawing the diagram by extending C to E such that CE is perpendicular to BE,

Here, let CE = h. Drawing AC,

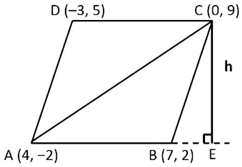
We need to find h.

In ∆ABC, area of ∆ABC is given by

Area(∆ABC) = 1/2 × base × height

= 1/2 × AB × h [∵ CE is the height of the triangle ABC, and CE = h] …(i)

We have x₁ = 4 and y₁ = -2,

x₂ = 7 and y₂ = 2,

x₃ = 0 and y₃ = 9

By coordinate geometry formula,

Putting in all the values, we get

⇒

Thus, AB = 5 …(ii)

Area of triangle is given by,

Area(∆ABC) =

= 1/2 [4(2 – 9) + 7(9 – (-2)) + 0(-2 – 2)]

= 1/2 [4 × -7 + 7 × 11 + 0]

= 1/2 [-28 + 77] = 1/2 × 49 = 49/2 …(iii)

Comparing equations (i) and (iii),

1/2 × AB × h = 49/2

⇒ AB × h = 49

⇒ 5 × h = 49 [by equation (ii)]

⇒ h = 9.8 units

Thus, length of the altitude of the parallelogram on the base AB is 9.8 units.