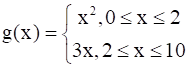The relation f is defined by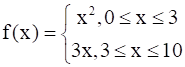

The relation g is defined by

Show that f is a function and g is not a function.

Given:

As

⇒ f(x) = x² for 0≤x<3

And f(x) = 3xfor 3≤x<10

At x = 3, f(x) = x² = 3² = 9

Also, at x = 3, f(x) = 3x = 3×3 = 9

Hence, we see for 0≤x≤10, f(x) has unique images. Thus, by definition of a function the given relation is function.

Now,

As

⇒ g(x) = x² for 0≤x<2

And g(x) = 3xfor 2≤x<10

At x = 2, g(x) = x² = 2² = 4

Also, at x = 2, g(x) = 3x = 3×2 = 6

Hence, element 2 of the domain of relation g(x) corresponds to two different images i.e. 4 and 6.

because for 0≤x≤10, f(x) does not have unique images. Thus, by definition of a function the given relation is not a function.