Prove that the lengths of tangents drawn from an external point to a circle are equal.

Given: CA and CB are two tangents drawn from an external point C to the circle with center O and radius r.

The figure is given as:

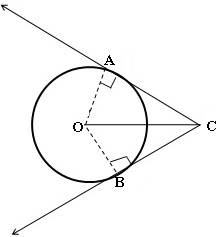
To prove: CA = CB

Firstly, join OC.

Proof:

Since, tangent to circle is perpendicular to the radius through the point of contact.

∴ ∠CAO = ∠CBO = 90°

In ΔCAO and ΔCOB,

CO = CO (Common in both the triangles)

AO = BO (Radius of the circle)

∠ CAO = ∠ CBO (90°)

∴ ΔCAO ≅ ΔCBO (by RHS congruence criterion)

⇒ CA = CB (by CPCT)

Thus, the lengths of the tangents drawn from an external point to a circle are equal.