The height of a cone is 10 cm. The cone is divided into two parts using a plane parallel to its base at the middle of its height. Find the ratio of the volumes of the two parts.
The figure is given below:
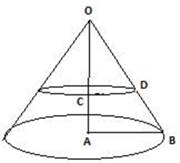
Height of cone = H = 10 cm
Let R be the radius of the given cone.
After dividing cone into two parts using a plane parallel to its base at the middle of its height, one part is cone and the other part formed is frustum.
Let r be the top radius of the frustum.
In right angled triangle OCD and OAB,
∠OCD = ∠OAB = 90°
∠COD = ∠AOB (common)
∴ ΔOCD ~ ΔOAB (AA similarity)
⇒ OA/OC = AB/CD = OB/OD
⇒ h/(h/2) = R/r
⇒ R = 2r
Height of the new cone formed = h = 10/2 = 5 cm
Volume of the new cone = (1/3)πr2h = (1/3) × π × (r)2 × (5)
= (5/3)πr2
Volume of the given cone = (1/3)πR2H
= (1/3)π(2r)2H
= (4/3)πr2(10)
= (40/3)πr2
∴ Height of frustum = H’ = 10/2 = 5 cm
Base Radius of frustum = R cm
Top radius of frustum = r = R/2 cm
Volume of frustum = Volume of given cone – Volume of new cone formed
= (40/3)πr2 - (5/3)πr2
= (35/3)πr2
Ratio of volume of two parts = Volume of new cone formed: Volume of frustum
= (5/3)πr2:(35/3)πr2 = 1:7
Therefore, the required ratio is 1:7.