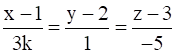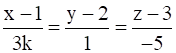If the lines 
and 
are perpendicular, find the value of k.
Two lines 
and 
are perpendicular to each other if
a1a2 + b1b2 + c1c2 = 0
Given -
comparing with
we get -
x1 =1, y1 = 2, z1 = 3
& a1 = - 3, b1 = 2k, c1 = 2
Similarly,
comparing with
we get -
x2 = 1, y2 = 2, z2 = 3
& a2 = 3k, b2 = 1, c2 = -5
Since the two lines are perpendicular,
a1a2 + b1b2 + c1c2 = 0
⇒ (-3) × 3k + 2k × 1 + 2 × (-5) = 0
⇒ -9k + 2k - 10 = 0
⇒ -7k = 10
∴ k = -10/7
Hence, the value of k is -10/7.
6