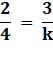If the system of equations 2x + 3y = 5, 4x + ky = 10 has infinitely many solutions, then k =

Given:

Equation 1: 2x + 3y = 5

Equation 2: 4x + ky = 10

Both the equations are in the form of :

a₁x + b₁y = c₁ & a₂x + b₂y = c₂ where

a₁ & a₂ are the coefficients of x

b₁ & b₂ are the coefficients of y

c₁ & c₂ are the constants

For the system of linear equations to have infinitely many solutions we must have

………(i)

According to the problem:

a₁ = 2

a₂ = 4

b₁ = 3

b₂ = k

c₁ = 5

c₂ = 10

Putting the above values in equation (i) and solving the extreme left and extreme right portion of the equality we get the value of a

⇒ 2k = 12 ⇒ k = 6

The value of k for which the system of equations has infinitely many solution is k = 6