The area of the triangle formed by the lines x = 3, y = 4 and x = y is
Given :
Equation 1: x = 3
Equation 2: y = 4
Equation 3: x = y
Equation 1 is a line parallel to y axis
Equation 2 is a line parallel to x axis
So Equation 1 & 2 are mutually perpendicular to each other.
Hence the triangle formed is a right angled triangle.
First we solve the three lines simultaneously by method of substitution and get the three points of intersection or three coordinates of the triangle.
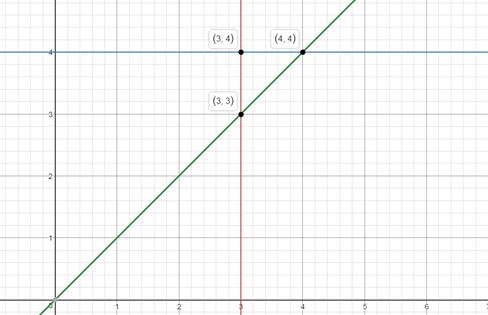
Solving Equation 1 & 2 we get the coordinate ( 3, 4 ). Let this Coordinate name be P1
Solving Equation 2 & 3 we get the coordinate ( 4 ,4 ). Let this Coordinate name be P2
Solving Equation 3 & 1 we get the coordinate ( 3 ,3 ). Let this Coordinate name be P3
We now use the formula for Area of a triangle through 3 given points
Area = ![]() *| x1 * (y2 – y3) + x2 * (y3 – y1) + x3 * (y1 – y2) |
*| x1 * (y2 – y3) + x2 * (y3 – y1) + x3 * (y1 – y2) |
Where x1 ,y1 are the coordinates of P1
x2, y2 are the coordinates of P2
x3 ,y3 are the coordinates of P3
Area of the Given Triangle = ![]() *| 3* (4– 3) + 4 * (3 – 4) + 3* (4– 4) |
*| 3* (4– 3) + 4 * (3 – 4) + 3* (4– 4) |
Area = ![]() *| 3* (1) + 4 * ( – 1) + 3* (0) |
*| 3* (1) + 4 * ( – 1) + 3* (0) |
Area = ![]() *| 3– 4 |⇒ Area =
*| 3– 4 |⇒ Area = ![]() sq. units
sq. units
The Area of the triangle is ![]() sq. units
sq. units