If S1 is the sum of an arithmetic progression of 'n' odd number of terms and S2 the sum of the terms of the series in odd places, then 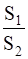 =
=
S1 = ![]() (2a + (n–1) d)
(2a + (n–1) d)
Out of these odd numbers of terms, there are ![]() terms in odd places
terms in odd places
S2 = ![]() (2a + (
(2a + (![]() –1) d)
–1) d)
Common difference of two odd places is 2d
S2 = ![]() (2a + (n–1) d)
(2a + (n–1) d)
Now,
![]() =
= ![]()
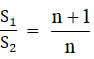
13