In figure 2.7 line /|| line m and line n|| line p. Find ∠ a, ∠ b, ∠ c from the given measure of an angle.

Question

Philoid · Accepted Answer

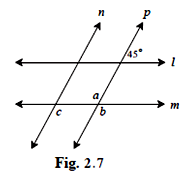
Given line L || line M and line P is transversal.

To find: ∠ a, ∠ b, ∠ c

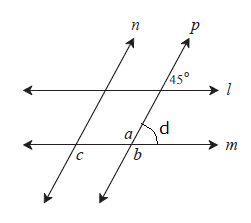
Construction: extend E and D in answer diagram

∠ e ≅ ∠ d (corresponding angle theorem) if two parallel line are cut by a transversal, then the pairs of corresponding angle are congruent.

� � �

∴ ∠ d = 45° (given above diagram)

∠ a + ∠ d = 180° (linear pair angle)

∠ a + 45° = 180°

∠ a = 180° -45°

∠ a = 135°

∠ a ≅ ∠ b (vertically opposite angles formed are congruent)

∴ ∠ b = 135°

Line N || line P and line M is transversal (given)

∴ ∠ b≅ ∠ c (corresponding angle theorem) if two parallel line are cut by a transversal, then the pairs of corresponding angle are congruent.

∴ ∠ c = 135°.