In figure 2.27, if line AB || line CF and line BC || line ED then prove that ∠ ABC = ∠ FDE

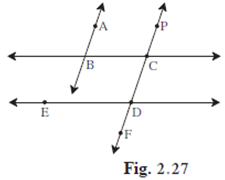
Given: Line AB ∥ CF and line BC ∥ ED

To find: ∠ ABC = ∠ FDE

Construction: G and h in diagram.

AB ∥ CD and BC is transversal both

So, ∠ ABC = ∠ PCG (linear pair angle)

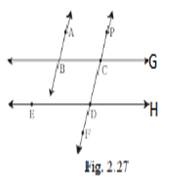
BC∥ ED and PF is transversal line to both

So, ∠ ECG = ∠ CDH

∠ CD = ∠ FDE (Both angle is opposite)

∴ ∠ ABC = ∠ FDE (hence proved)