Diameter of a circle is 26 cm and length of a chord of the circle is 24 cm. Find the distance of the chord from the center.

Question

Philoid · Accepted Answer

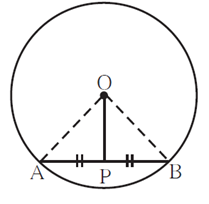
Given that diameter = 26cm

Radius = Diameter / 2 = 26 /2 = 13cm

So, OA = 13cm

And AB = 24 cm

We know that a perpendicular drawn from the center of a circle on its chord bisects

the chord.

∴ AP = PB = 12 cm

In the right angled ΔOAP using Pythagoras theorem,

⇒ OA² = OP² + AP²

⇒ 13² = OP² + 12²

⇒ 169 = OP² + 144

⇒ OP² = 25

⇒ OP = 5cm

So, the distance of chord from the center is 5cm.